CoL Inquiry 2025 - Part Six

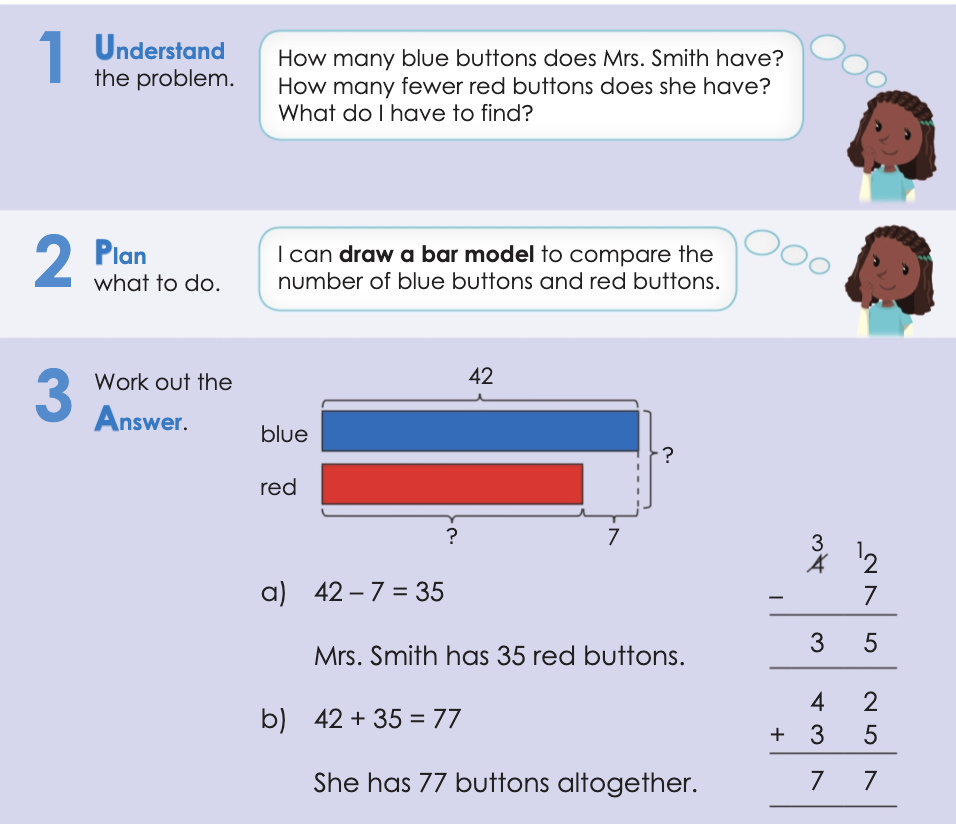
In order to gain quantitative data I constructed a customised eAsttle test for my inquiry group to take. It would assess Number Knowledge, Number Strategy, and Algebra. The results, while they don't indicate a massive shift in overall progress are incredibly affirming. They confirm that my previous focus on improving comprehension of whole number and single-step problems was the correct priority.

This has established a strong foundation: The group demonstrated 100% success in procedural objectives like "Model and solve linear, simultaneous & simple quadratic equations." They also performed strongly in finding and expressing rules for number sequences. When the language is direct and tells them what to do (solve, model, find a rule), they now execute confidently.

This is a significant positive step. Our work has clearly improved their ability to translate straightforward narrative into the correct mathematical procedures, which is critical for problem solving.

 The beauty of these results is how they align perfectly with the current curriculum map. The most significant gaps revealed by the test are in topics we simply haven't covered yet in our Pr1me program. I don't look at it as a failure in my current teaching; it's a powerful
alert about where I need to proactively prepare the students' language skills.

The biggest gaps (within the focus areas) sit in the three major concepts that Pr1me will introduce later this year:

• Negative Numbers: The largest gap is "Explain the meaning of negative numbers" (69% Gaps).
• Decimals: There's a 50% Gaps rate in "Write & solve whole number/decimal problems using all four operations."
• Fractions: Students struggled with "Write/solve story problems involving basic fractions" (25% Gaps).

The data tells me that when Pr1me introduces these units, the content itself will be the secondary problem; the primary barrier will still be the complex language because it's more abstract and intricate than the whole number problems they've mastered. They need to understand the words before they can do the math.

The comparison of the earlier diagnostic tests to our recent e-asTTle results has been the most powerful validation of my inquiry cycle yet. The data confirms what I hoped: the strategic focus on comprehension and whole-number strategy has successfully closed old gaps, providing a strong foundation for the Pr1me program.

Here is a quick look at where each student has shifted in their Number Knowledge and Strategy since the start of the year, followed by an analysis of the group's overall progress.

Individual Progress Snapshot: Closing Gaps

Student (Current Level) Key Improvement Area (Strategy/Comprehension) Remaining Challenge (New Barrier)

Student A (3P) Clear Word Problem Gain: They've overcome the language barriers they had in simple multiplication and division word problems. They are now successfully translating simple narratives. Large Number Language: The comprehension barrier remains for place value in large whole numbers and the conceptual language of fractions.

Student B (2A) Procedural Clarity: Johan gained competence in the language of order of operations and is successfully translating simple word problems. They've overcome their earlier struggles with visual strategies like number lines. Foundational Facts & Fractions: They're still struggling with basic addition/subtraction facts and the complex translational language required by fractions.

Student C (3B) Procedural/Algebraic Language: They shows strong gains in understanding the language of order of operations and the procedural concepts of powers of whole numbers. Fractional and Conceptual Language: The language of simple fractions is still a consistent barrier, as is the abstract definition of negative numbers.

Student D (3B) Place Value Mastery: They've successfully overcame their early struggles with interpreting the language of place value and is now applying that understanding to decimals. Translational Fraction Barrier: Their most consistent weakness is the inability to translate a word problem that includes a fractional quantity into an equation.

Student F (3P) Fractional Head Start: They are unique—they've showed success in the initial stages of fraction word problem translation, an area of difficulty for the rest of the group. They've made strong gains in procedural language. Algebraic Patterns: Their remaining weakness is translating the language of patterns and sequential rules, suggesting a distinct type of abstract language comprehension issue.

Student G (3B) Strategy/Procedural Gain: They've successfully transitioned from struggling with simple division word problems to mastering order of operations. Their highest score in Algebra shows excellent procedural command. Fragile Conceptual Language: Their understanding of negative numbers is fragile, indicating that the language used to define and apply the concept needs dedicated reinforcement.

Student H (3B) Strong Strategy Gains: They've moved from struggling with simple division to mastering multi-step problem combinations. This is the clearest example of a direct win for my inquiry on comprehension and translation. Advanced Algebraic Comprehension: Their struggles with the language required to use a rule to make predictions and describe patterns in sequence.

The comparison of the earlier PAT test results from the start of the year provides strong evidence that my inquiry cycle focusing on comprehension and whole-number strategy has been effective. We've successfully built the necessary language bridge.

1. Number Knowledge Progress: Success in Foundational Language

Positive Shift : Nearly all students have significantly improved their ability to read and interpret the language of place value in whole numbers and are now successfully applying that foundational language to decimal place value. This is a big leap from the initial struggles we saw at the start of the year.

2. Strategy (Number Sense & Operations) Progress: Mastery of Simple Translation

Positive Shift : Every single student who initially struggled with single-step, whole-number word problems is now scoring highly or achieving in "Write & solve whole number story problems." The most significant result is their successful transition to solving problems with combinations of operations. The language decoding for simple arithmetic is now working.

Next Barrier : The strategy breakdown occurs when students must translate a multi-step word problem that also contains complex number language (fractions, decimals). The inability to "Solve problems using fractions of whole numbers or decimals" is the new strategic weakness, showing that the strategy itself needs a more advanced layer of comprehension.

The work we've done has provided the necessary language bridge to move from non-comprehension to solid procedural understanding in foundational arithmetic. My next step—pre-teaching the language of upcoming complex units (fractions, decimals, negatives) before the Pr1me program introduces them—is perfectly validated by where their progress is currently stalling. My inquiry remains focused on comprehension, but it must now shift from addressing prior gaps to proactive preparation for upcoming units.

A revitalised look at my inquiry focus is: How can I use explicit literacy strategies to pre-teach the conceptual and translational vocabulary of concepts? I will be tracking my target group as I learn to better support them, not by teaching ahead of the Pr1me program, but by teaching the language of the concepts ahead of it. The goal is to improve their literacy toolkit so they can tackle new concepts with greater confidence.

The journey continues, and the data confirms I am focused on the right path for supporting my students' mathematical language development.

CoL Inquiry 2025 - Part Five

 As part of our inquiry cycle we have the opportunity to use an awesome tool called Vosaic. Vosaic allows teachers to record and upload lessons, and it's AI tool is able to analyse the lesson, looking for specific elements depending on the prompts it has been given.

We did a lesson which focused on estimation, front-end, and rounding.

I am unable to upload the video; it ended up being a 30 minute session, but here are the findings of the lesson. If you would like to watch the whole lesson, please email me and I can share it with you.

Vosaic:
"Analysis of Maths Vocabulary Use in the Lesson

The teacher effectively supports students in learning and using mathematical vocabulary throughout the lesson on estimating products. Here are some key strategies observed:

Explicit Definitions: The teacher begins by defining key terms such as "estimating" and "product." For example, at  → , the teacher asks, "who remembers what estimating means?" and reinforces the definition by stating it involves finding an "approximate answer" ( → ).

Contextual Usage: The teacher uses vocabulary in context, such as explaining that "product" refers to the answer of a multiplication problem ( → ). This contextualization helps students understand how the terms apply to their work.

Repetition and Reinforcement: The teacher frequently revisits key terms throughout the lesson. For instance, the term "rounding" is mentioned multiple times ( → ,  → ), reinforcing its importance in the estimation process.

Encouraging Student Responses: The teacher prompts students to use the vocabulary themselves, asking questions like, "What does reasonable mean?" ( → ) and "Which of the two numbers, 45 or 2, are we rounding?" ( → ). This encourages active participation and reinforces their understanding of the terms.

Visual and Practical Examples: The teacher provides practical examples of how to apply the vocabulary in calculations, such as rounding numbers and estimating products (e.g., 45 rounded to 50 at  → ). This hands-on approach helps solidify their understanding.

Comparative Analysis: The teacher contrasts different estimation methods, such as rounding versus front-end estimation ( → ). This comparison not only clarifies the vocabulary but also helps students understand when to use each method effectively.

Overall, the teacher's approach to using mathematical vocabulary is systematic and interactive, fostering an environment where students can learn and apply the language of mathematics confidently.

Research: Research indicates that explicit vocabulary instruction, contextual learning, and active engagement are effective strategies for enhancing students' understanding of mathematical language (Beck, McKeown, & Kucan, 2013). Additionally, encouraging students to articulate their understanding through discussion and practice can significantly improve their mathematical literacy (Hiebert & Wearne, 2003).

Reflections:
I felt really positive after reading this; it can sometimes be hard when you are in the midst of the lesson, to ensure you are doing the little things right; for me the focus is on the language, and vocabulary; for the students it is to learn and reflect on their prior knowledge of the topic. Ensuring that I am covering both aspects is critically important, as I don't want to lose sight of the goals for either students, or myself.

CoL Inquiry 2025 - Part Four

 Part of the challenge this year has been that my students are very capable of solving word problems when they are scaffolded, and I guide them through the steps.

What I need for them to be able to do is to independently identify what procedures they need to complete in order to successfully solve the word problems.

I decided it was necessary to provide my students with a guide book; a set of slides which would support them in determining what kind of word problem they have been given. This guide supports students to read questions, to categorise them, and then to apply the correct strategy.

Once they have categorised the question they will be able to apply their strategies. I found this more effective than my previous iteration of this; 

The reason being, if I simply give them the key words in the question they are constantly searching just for the words that they need, rather than comprehending the scenario/story. By understanding the scenario and the context in which the problem occurs they are able to apply strategies like visualisation that can help them to make sense of the question itself, and in turn, make it easier to solve the problem. 

By consolidating the reading, visualisation and application of strategy my students have shown an improved understanding and confidence when it comes to independently solving problems.

I am going to ensure they have access to these slides so they are able to rewind it and use it when they need it. The next steps are going to be to continue reinforcing the specific terminology and vocabulary used in each concept.

CoL 2025 - Part Three

This year, we've been working hard to implement a more structured approach to maths using the PR1ME Maths program, which I’ve found incredibly helpful for building strong number sense and step-by-step thinking in students. Each lesson scaffolds understanding clearly—Understand the Problem, Plan what to do, Work out the Answer—and students respond well to the predictable structure.

But I started to notice something. Despite the structure, many students were still getting stuck on multi-step problems, especially when the wording got tricky. Even with a model or clear number strategy, some students weren’t quite sure what was actually happening in the problem.

That’s when I decided to trial the 3 Reads Protocol alongside PR1ME. 

What is the 3 Reads Protocol?

It’s a comprehension strategy borrowed from literacy and adapted for maths word problems.

1.  What is the problem about?

(Just the context—no numbers yet. Are we talking about muffins? Trains? People?)

2.  What is the problem asking?

(Focus on the question. What are we meant to find out?)

3.  What are the important numbers or facts?

(What do we need to solve the problem? Which strategy might work?)

How Does This Compare to PR1ME’s Approach?

The PR1ME problem-solving routine (like the image above) follows a similar flow:

1. Understand the Problem; Students are prompted to ask questions:

How many blue buttons? How many fewer red? What do I need to find?

2. Plan what to do; They draw a bar model, or visualise with a known strategy.

3. Work out the answer They solve, step-by-step.

There are a number of similarities in each of the protocols:

- Encourage thinking before solving

- Focus on the story behind the numbers

- Encourage visual strategies like drawing or bar models

- Build mathematical language through questioning

But here’s the key difference:

👉 The 3 Reads Protocol slows down the reading comprehension process even more.

It makes students treat the problem like a piece of reading rather than just a maths equation hiding in a story. Strategies which can then be applied are to use manipulatives, or visualisation strategies like bar models that can help students turn a confusing question into a problem they can understand and solve without needing as much reading comprehension.

In practice:

In large group/class instruction, I stuck to the PR1ME structure, as it aligns with the scope and expectations of our program. The vocabulary and worked examples help all students—especially those who thrive with repetition and visual modelling.

We’ll continue using both. The PR1ME problem-solving routine is here to stay—it’s well-structured, scaffolded, and clearly links to our curriculum refresh.

But I see real value in making room for the 3 Reads Protocol in:

- Small group problem-solving

- Mixed-ability collaborative tasks

- Problem-solving challenges or rich tasks

In short:

We’re not replacing one with the other. We’re building a toolkit—and giving students more ways to understand, approach, and solve.

I am excited to see the results of this; we have had a very staggered end of term, but moving into the next term we will administer a Chapter Test which will require students to solve word problems; am unsure how well they will be able to independently apply the protocol. We will continue to build on this in Term 3.

If you’re noticing students can’t make sense of the maths problem even though they know the strategy, try the 3 Reads approach. Sometimes the barrier isn’t the maths—it’s the language.

CoL 2025 - Part Two

Conversations with my colleagues have been different this year compared to last year; a brand new curriculum document, and structured maths programs have meant that a lot of us are still in the learning stages too - having to familiarise ourselves with new pedagogies, vocabulary, and realising that there is a great of work to cover before our students can perform at the expected level under the new curriculum.

What has not changed is the common struggle; our students are struggling to solve word problems independently. I have discussed this with colleagues in the junior and senior school and with CoL colleagues working at secondary level and it a common thread with students in our schools. 

They have been taught the strategies, can apply them in supported environments, can solve linear problems very easily, however when the problems add multiple steps, or are phrased in a way which challenges students ability to comprehend or infer the obvious path to solving the problem they are unable to apply their known strategies confidently.

Let's look at some examples taken from the Pr1me Practice Books

Example Question One:

A shopkeeper has 378 apples, and 53 oranges. How many apples and oranges does the shopkeeper have altogether?

Straightforward. Linear problem solving. Clear numbers of objects, clear scenario, and a key word which indicates to the students clearly which operation/strategy they need to apply. The reality of problem solving in questions like this is that problems like this do not require much of a problem to be solved. The question is a straightforward story, no twists, no turns, just straightforward combining of two numbers to find a total. 

The very next question:

After selling 185 muffins, a bakery had 269 muffins left. How many muffins did the bakery have at first?

Questions like this require students to understand the story of the problem before they are able to even think of which strategy to apply. The question requires the same mathematical strategy, it is just simple addition, right? 185 + 269 = 454 - however this problem caused confusion, and I wondered why.

I have a hunch, I'll talk about it in the next blog post. Stay tuned to see how we address this.

CoL 2025 - Part One

This is my third year reflecting on this very same question; How can I support my lower literacy students with their comprehension of word problems in maths?

Last year I thought I'd worked out an effective solution; use the CPA approach to strengthen their foundational and conceptual understanding, however there was a limitation in this. Most frequently the A in CPA was symbolic, it was using digits, numbers, and operational symbols. It did not address the hole in their understanding that was decoding, and comprehending what the word problems they faced were asking of them. 

 

For the first time since I began teaching I have struggled to find a focus for my inquiry; not because I haven't identified areas in my student's learning that needs further support, but because for the first time in my own career I am teaching to a structured program.

This year, like all of you, I have been tasked with rolling out a structured Maths program, in our case Scholastic's Pr1me Mathematics, and boy has it been a learning curve. 

First, let me start by saying I am thoroughly enjoying the program so far; as someone who can be very pedantic about the resources I use in my class I have spent countless hours trying to create learning experiences that are engaging, interesting, and enjoyable for my students to use. Pr1me has done an incredible job of taking that job off my hands.

However, it is through the using of resources not produced by me that I encountered the first obstacle for my students. The first part of the Pr1me program is a diagnostic test. This test is used to determine which Book of the program the students will take on for they year. For our students this was a gruelling experience. 14 pages, back and front. Writing with pencils, instead of their mouse. Questions with a wide variety of difficulties, some straightforward, some multi-step problem solving. This was definitely not something our students were used to. The results of the test spoke for themselves; most students answered between 5-10 of the 30+ questions in the test with some accuracy, or indication of strategic thinking.

After they finished the test, we did a little bit of a debrief; 

How did you find the test? What was the hardest part about it? What did you find most confusing?

There were a wide range of answers, however the fundamental theme throughout them was a lack of understanding around what the question was actually asking them to do. 

I rewrote 3 questions on the board, mimicking the style of questions they had just done in the test. We went through it together, drawing out the key numbers, and finding the operative words in the question. With plenty of support and guidance we ended up turning the word problem into a numerical equation, that the students were able to very easily solve using strategies they had been learning with me.

So where's the barrier; what is it that they are not understanding? It has to be the words. It just has to.

So; here our journey begins. I'm narrowing down my target group, but I am going to look at the students in my class with lower level literacy, and low level of maths, and tracking their progress, as I learn to better support them, now with the structure, (or restrictions) of the Pr1me program.

Follow along to see where how far we'll go!

CoL Inquiry - Using Evidence to Guide Practice - Part Five

My math practice this year has made considerable changes; personally I like I've grown in confidence with my practice, the research, the conversations (with colleagues and students), reflections, and all of it has left me feeling more capable as a teacher, and it has translated into students who feel much more confident and are enjoying math. One of the pieces of qualitative data I gathered at the start of my inquiry was their voice; how were they feeling about maths; here's what they said.

I will be reissuing this same questionnaire this week, and I am super excited to see the results; in speaking with my students they are feeling more capable, and demonstrate this on a regular basis in class.

In terms of data the previous blog post has what we have done so far, eAsttle test provided me next steps, and Gloss testing is being done - as I write this I am nearly finished with my inquiry group, and even without another Gloss Test from the start of the year (reminding myself how good they are, and that I need to do more of them)  I can feel their conceptual understanding has improved. In terms of quantitative results, I have now tested 6 of the students in my inquiry group. Each of them has reached Stage 6 in Addition/Subtraction, most, if not all have reached Stage 5+ in Multiplication and division. 

This still means they are working towards achieving at the level that they should be, however, they have all shifted upwards; their OTJs had them placed at Year 4, some early, some late, but definitely below the expected level. A single test is not indicative of their progress, but I can't help but be excited to see this acceleration.